Linear subspace
The concept of a linear subspace (or vector subspace) is important in linear algebra and related fields of mathematics. A linear subspace is usually called simply a subspace when the context serves to distinguish it from other kinds of subspaces.
Contents |
Definition and useful characterization and subspace
Let K be a field (such as the field of real numbers), and let V be a vector space over K. As usual, we call elements of V vectors and call elements of K scalars. Suppose that W is a subset of V. If W is a vector space itself, with the same vector space operations as V has, then it is a subspace of V.
To use this definition, we don't have to prove that all the properties of a vector space hold for W. Instead, we can prove a theorem that gives us an easier way to show that a subset of a vector space is a subspace.
Theorem: Let V be a vector space over the field K, and let W be a subset of V. Then W is a subspace if and only if it satisfies the following three conditions:
- The zero vector, 0, is in W.
- If u and v are elements of W, then any linear combination of u and v is an element of W;
- If u is an element of W and c is a scalar from K, then the scalar product cu is an element of W;
Proof: Firstly, property 1 ensures W is nonempty. Looking at the definition of a vector space, we see that properties 2 and 3 above assure closure of W under addition and scalar multiplication, so the vector space operations are well defined. Since elements of W are necessarily elements of V, axioms 1, 2 and 5-8 of a vector space are satisfied. By the closure of W under scalar multiplication (specifically by 0 and -1), axioms 3 and 4 of a vector space are satisfied.
Conversely, if W is subspace of V, then W is itself a vector space under the operations induced by V, so properties 2 and 3 are satisfied. By property 3, -w is in W whenever w is, and it follows that W is closed under subtraction as well. Since W is nonempty, there is an element x in W, and 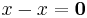 is in W, so property 1 is satisfied. One can also argue that since W is nonempty, there is an element x in W, and 0 is in the field K so
is in W, so property 1 is satisfied. One can also argue that since W is nonempty, there is an element x in W, and 0 is in the field K so 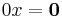 and therefore property 1 is satisfied.
and therefore property 1 is satisfied.
Example I: Let the field K be the set R of real numbers, and let the vector space V be the Euclidean space R3. Take W to be the set of all vectors in V whose last component is 0. Then W is a subspace of V.
Proof:
- Given u and v in W, then they can be expressed as u = (u1,u2,0) and v = (v1,v2,0). Then u + v = (u1+v1,u2+v2,0+0) = (u1+v1,u2+v2,0). Thus, u + v is an element of W, too.
- Given u in W and a scalar c in R, if u = (u1,u2,0) again, then cu = (cu1, cu2, c0) = (cu1,cu2,0). Thus, cu is an element of W too.
Example II: Let the field be R again, but now let the vector space be the Euclidean geometry R2. Take W to be the set of points (x,y) of R2 such that x = y. Then W is a subspace of R2.
Proof:
- Let p = (p1,p2) and q = (q1,q2) be elements of W, that is, points in the plane such that p1 = p2 and q1 = q2. Then p + q = (p1+q1,p2+q2); since p1 = p2 and q1 = q2, then p1 + q1 = p2 + q2, so p + q is an element of W.
- Let p = (p1,p2) be an element of W, that is, a point in the plane such that p1 = p2, and let c be a scalar in R. Then cp = (cp1,cp2); since p1 = p2, then cp1 = cp2, so cp is an element of W.
In general, any subset of a Euclidean space Rn that is defined by a system of homogeneous linear equations will yield a subspace. (The equation in example I was z = 0, and the equation in example II was x = y.) Geometrically, these subspaces are points, lines, planes, and so on, that pass through the point 0.
Example III: Again take the field to be R, but now let the vector space V be the set RR of all functions from R to R. Let C(R) be the subset consisting of continuous functions. Then C(R) is a subspace of RR.
Proof:
- We know from calculus that 0 ∈ C(R) ⊂ RR.
- We know from calculus the sum of continuous functions is continuous.
- Again, we know from calculus that the product of a continuous function and a number is continuous.
Example IV: Keep the same field and vector space as before, but now consider the set Diff(R) of all differentiable functions. The same sort of argument as before shows that this is a subspace too.
Examples that extend these themes are common in functional analysis.
Properties of subspaces
A way to characterize subspaces is that they are closed under linear combinations. That is, a nonempty set W is a subspace if and only if every linear combination of (finitely many) elements of W also belongs to W. Conditions 2 and 3 for a subspace are simply the most basic kinds of linear combinations.
Operations on subspaces
Given subspaces U and W of a vector space V, then their intersection U ∩ W := {v ∈ V : v is an element of both U and W} is also a subspace of V.
Proof:
- Let v and w be elements of U ∩ W. Then v and w belong to both U and W. Because U is a subspace, then v + w belongs to U. Similarly, since W is a subspace, then v + w belongs to W. Thus, v + w belongs to U ∩ W.
- Let v belong to U ∩ W, and let c be a scalar. Then v belongs to both U and W. Since U and W are subspaces, cv belongs to both U and W.
- Since U and W are vector spaces, then 0 belongs to both sets. Thus, 0 belongs to U ∩ W.
For every vector space V, the set {0} and V itself are subspaces of V.
If V is an inner product space, then the orthogonal complement of any subspace of V is again a subspace.